I have been a math teacher since 1991 when I taught my first algebra class at Philadelphia Community College. I had just received my Bachelors degree in Physics. Bolstered by my girlfriend Val's seemingly cushy part-time employment as a math instructor, and the fact that the math department was in quick need of an algebra instructor, I interviewed with the math chairman, and convinced him that I would be perfect for the job.
I was right. As it turned out, I was good at it. Not that I didn't have my problems, I had many. However, I seemed to have a rapport with a class of math students that allowed me to teach in a relaxed atmosphere and keep everyone engaged. I have always enjoyed teaching and felt lucky to have had the kind of job that continually allows me to learn as much as my students.
But I work hard at teaching. More than most, I think, but it may be that every teacher thinks that. I know there are alot of people who look at teachers and say, "Boy, what a job, summers off." These folks think that it's an easy task to walk in a room, stand up in front of 45 young people, and keep them directly engaged in mathematics for 90 minutes three to five days a week. Plus, they don't think about all the lost nights and weekends a teacher spends preparing exercies and grading papers.
Preparing and psyching up for the experience of teaching is not only exciting, but scary too. As a musician, I've played in countless bands, and I gained some experience on stage. I can liken the first day of a new class to the same kind of butterflies that one can get before Saturday nite's performance.
To keep my anxiety at a minimum, I have always prepared intensely for all my classes, producing notes, websites, hand-outs, transparencies, examples, and finding news stories relevant to our topics. I have learned how to create websites, and use the Internet (significant as I am no adolescent.) and create online classes. I have learned how to create a syllabus of information, pace it through the semester, and determine whether or not it's being understood.
But the biggest thing I've learned from teaching is patience. Early on, I would start to lose it when students would not understand what I was s-o-c-a-r-e-f-u-l-l-y-t-e-l-l-i-n-g-t-h-e-m. I didn't know why they asked the same thing over and over again.
I had to learn that each student's mind will absorb the patterns of math differently, and that I have to frame each concept so that it may be understood as quickly as each mind can possibly get it. It's somewhat like using the right phrase that instantly communicates the message, and the student grasps the pattern all at once in a simple and clear understanding. Finding those key words, and saying them in the right tone is the Teacher's Holy Grail for which there is no resolution. Each semester, the new class of students enlarges the catalogue of Magick Words, and we all climb the Mountain of Math together.
My subject is greeted with much noise and moaning. "Aaaawrrhhh, math…." eyes rolling, head twisting, soul writing in agony at the thought of math class. "Why do we have to learn this?" or "What good will this ever be?" they whine.
I have answered that question with a plethora of responses:
It's a workout for your left head muscle.
You never know what you might be doing in the future.
It's history.
It's cool.
Someday, somebody could pay you to tell them what's in these books.
And while I still believe that math and science are an important part of every educated mind, I've had problems being motivated to teach the topics given in the basic curriculum.
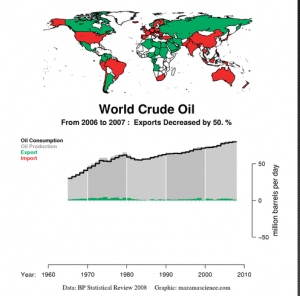
After learning about Peak Oil, and then, economic imbalances, topped off with ecological collapse, what good did learning to solve equations with rational expressions do? How does spending two weeks of precious classtime on factoring prepare student to think critically?
I admit, I'd had reservations about college math curricula even before I'd learned about the impending slide of civilization. Any criticism or suggestion of restructure would be met by the math department with " Well they have to learn this."
"But, why?", I'd ask.
"Because they're learning critical thinking." was always the last response.
Nowhere have I ever found evidence of that claim.
So what then? What should my motivation to teach algebra, and the students' learning it, be?
Personally, I find the subject fascinating. The manipulation of tiny symbolic squiggles representing the unknown quantities of the universe dancing about a page is akin to a beautiful work of art or music. And I have always tried to communicate my own fascination and love of this subject, but many young college students just don't see it that way.
But more importantly, how will learning math help students navigate the challenges they are most certainly going to face as they live their lives in the coming years?
The easiest answer is to use mathematics to help students understand what is happening in the first place. In a class of Pre-algebra or general Algebra, the math topics are rudimentary, but amenable to using energy and population data for percent problems and linear equations. This kind of data is perfect for descriptive statistics analysis as well.
In a liberal arts math course, one can go even further. Looking at exponentials, compound interest, and annuity equations leads directly to the finite resource equation and finding the exponential reserve, which gives the amount of time left for a finite resource that is being used at an increasing percent annually. This allows analysis of gas, coal, oil, and even domestic wellwater timeframes.
In this way, by using actual data and mathematical analysis, communicating to students a realistic picture of the world outside the classroom is neither political, or, makes the teacher sound like a nut case.
Beyond that, re-learning all the skills lost by our cheap oil-cheap imports society will be a difficult task. If some Peak Oil theorists are right, we're going to have to learn to do many forgotten tasks ourselves. How much power can we get out of a nearby stream? How would we build a hydro-electric system?
Indeed, mathematics in a post-crash world will be used in carpentry, agriculture, domestic item production, civic engineering, food storage, the list is endless. McLuhan wrote we are returning to a cultural oral bias, this time with our eyes wide open. Perhaps we will have to re-live the entire history of mathematics from it's first applications to commerce and agriculture millenia ago in order to succeed in preserving our evolving culture.
In any case, mathematics curriculum must adapt to a post-oil reality, or the institutions that push it will be relegated to the dust bin. If only schools and universities just listened to their students asking "Why math?", and responded honestly, they would be much more successful in graduating productive students with higher quantitative and critical thinking skills. And we would all be better off as a society at large.